When multiplying fractions in order to find the product of two or more fractions, you just need to follow these three simple steps basically. Take the quiz to see how much you know!
Quiz completed 0 times
Step 1: Multiply the numerators together. The numerators are also called top numbers.
Step 2: Multiply the denominators together. The denominators are also called bottom numbers.
Step 3: Finally, try to simplify the product if needed to get the final answer.

For example, notice what we do when we multiply the following fractions: 3/4 × 4/6.
Step 1: Multiply 3 and 4 to get 12 and 12 is the numerator of the product
Step 2: Multiply 4 and 6 to get 24 and 24 is the denominator of the product
3/4 × 4/6 = (3 × 4)/(4 × 6) = 12/24
Step 3: Divide both the numerator and the denominator by 12 to simplify the fraction. 12 is the greatest common factor (GCF) of 12 and 24.
3/4 × 4/6 = 1/2
The example above is straightforward. However, when multiplying fractions, you may wonder about the following cases.
- Multiplying fractions with different denominators
- Multiplying fractions with the same denominator
- Multiplying fractions with whole numbers
- Multiplying fractions with mixed numbers
- Multiplying improper fractions
Depending on which situation(s) you encounter, there are rules to follow when you multiply fractions with different types of fractions .
Rules of multiplying fractions
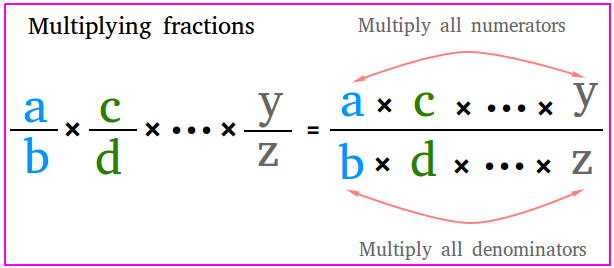
Rule 1: The most important rule is to multiply straight across. In other words, multiply the numerators to get the new numerator or the numerator of the product. Multiply the denominators to get the new denominator or the denominator of the product.
Rule 2: Another important rule is to always convert mixed fractions, also called mixed numbers into improper fractions before multiplying.
Rule 3: Convert whole numbers into fractions before doing multiplication.
Rule 4: Multiplying fractions is not the same as adding fractions. Therefore, you must not look for the least common denominator!
Rule 5: Simplify the product or write the fraction you end with after performing multiplication in lowest terms if needed.
Multiplying fractions with different denominators
When you multiply fractions with different denominators, just keep in mind rule 4 stated above. Do not look for a common denominator! The rule for adding fractions and multiplying fractions are not the same.
For example, notice that we do not look for a common denominator when we multiply the following fractions: 1/5 × 2/3.
Step 1: Multiply 1 and 2 to get 2
Step 2: Multiply 5 and 3 to get 15
1/5 × 2/3 = (1 × 2)/(5 × 3) = 2/15
Step 3: 2/15 is already written in lowest terms since the greatest common factor of 2 and 15 is 1.
1/5 × 2/3 = 1/2
Multiplying fractions with the same denominator
When you multiply fractions with the same denominator, just do the same thing you do when the fractions have unlike denominators.
Example: Multiply 3/4 and 1/4
3/4 × 1/4 = (3 × 1)/(4 × 4) = 3/16
Multiplying fractions with whole numbers
When you multiply fractions with whole numbers, just keep in mind rule 3 stated above. Convert the whole number into a fraction before doing multiplication.
Notice that any whole number x can be written as a fraction x/1 since any number divided by 1 will return the same number.
For example if you multiply the whole number 5 by another fraction, write 5 as 5/1 before you multiply.
Example: Multiply 5 and 2/3
5 × 2/3 = 5/1 × 2/3
5 × 2/3 = (5 × 2)/(1 × 3) = 10/3
Multiplying fractions with mixed numbers
When multiplying fractions with mixed numbers, it is important to remember rule 2. You must first convert any mixed number into a fraction before you multiply.
Suppose you are multiplying a fraction by 2 1/3. Since 2 1/3 is a mixed number, you must convert it into a fraction.
2 1/3 = (2 × 3 + 1)/3 = (6 + 1) / 3 = 7/3
Example: Multiply 1/6 and 2 1/3
1/6 × 2 1/3 = 1/6 × 7/3
1/6 × 7/3 = (1 × 7)/(6 × 3) = 7/18
Multiplying improper fractions
The multiplication of improper fractions is performed by following rule 1. Just multiply straight across. One thing you definitely do not want to do here is to convert the improper fractions to mixed numbers.
This will be very counterproductive as you will have to convert them right back into improper fractions.
Example: Multiply 9/2 and 3/5
9/2 × 3/5 = (9 × 3)/(2 × 5) = 27/10
A couple of tips and trick to follow when multiplying fractions
1. I recommend that you become familiar with the multiplication table. You will be able to perform the multiplication of fractions much quicker.
2. Sometimes, it is a good idea to simplify the fractions before multiplying to make calculations easier.
Take a look at the following example:
10
20
×
3
15
You can simplify 10/20 as 1/2 by dividing both 10 and 20 by 10.
You can simplify 3/15 as 1/5 by dividing both 3 and 15 by 3.
10
20
×
3
15
=
1
2
×
1
5
1
2
×
1
5
=
(1×1)
(5×1)
=
1
10
3. If you have three or more fractions, just multiply all numerators and all denominators
Going a little deeper! Why do we multiply fractions straight across?
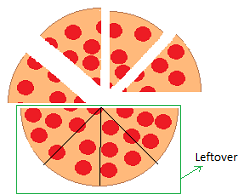
I would like to introduce the topic with an interesting example about pizza.
Suppose that you bought a medium pizza and the pizza has 8 slices.
4
8
1
2
1
4
of the leftover.
1
2
1
8
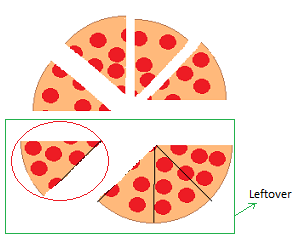
Thus, we can see that eating 1/4 of 1/2 is the same as eating 1/8.
1
8
is to perform the following multiplication:
We get this answer by multiplying the numbers on top (numerators): 1 × 1 = 1
and by multiplying the numbers at the bottom (denominators): 4 × 2 = 8
This is an interesting result but all you need to remember is the following:
When you multiply fractions, you must multiply straight across.
When the word ‘of‘ is placed between two fractions, it means multiplication.
