Jennifer Wilson, Senior Director, Implementation Portfolio
When teachers are curious about and trust student thinking to drive learning, they create classrooms where students learn mathematics by making sense of problems, learn through collaboration, and value each other’s thinking. These and other elements of problem-based teaching and learning help foster a world where students know, use, and enjoy mathematics.
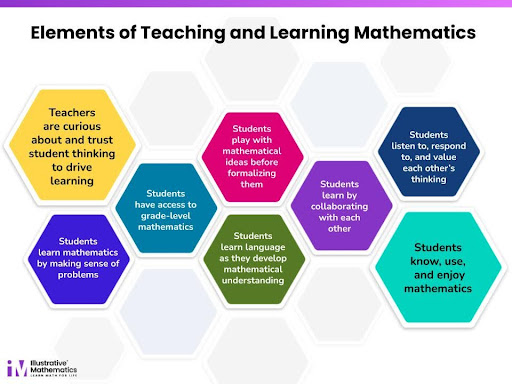
Getting students to talk about math is no easy task. How do we teach students to listen to, respond to, and value each other’s thinking?
When I first learned about Think-Pair-Share years ago, I was apprehensive about trying it with my students. Frankly, the thought of using the phrase “think-pair-share” with high school students made me feel silly.
But just like many of you, I had an active class with many students who were more interested in talking with each other—sometimes about math, sometimes not—than contributing to a whole class conversation. I realize now that I tended to call on students who responded “first and fast,” inadvertently sending the message that math was about getting the correct answer and getting it quickly. In small groups, students felt less pressure to be accurate and could develop their ideas. But in front of the whole class, if their idea didn’t come fast and with confidence in its accuracy, they were reluctant to share.
I knew something had to change in the way that we learned alongside each other, and so after a few nights of lost sleep, I arranged a class meeting. I invited students to share what they needed from their mathematical community when they’re learning math. It was enlightening to see that many of the things my students valued were the same practices I thought were missing in our time together.

I saw communicating, cooperating, talking, participating, and strategies, but what struck me most from their suggestions was the word everyone. After more conversation we agreed:
Everyone . . .
- Respects
- Contributes
- Listens
- Questions
- Collaborates
- Communicates
I let them know that I would help the class lean into these agreements by adding some structure to our conversations using the Think-Pair-Share routine.
When facilitating Think-Pair-Share, we first provide time for students to THINK. This step is so simple that it is often overlooked. Giving students a silent minute or two of independent think time to consider a problem is essential for creating the space students need to actively engage in the mathematics.
Next, students PAIR to discuss their thinking with a partner or in a small group. Students don’t all need to have an answer before they pair. Learning is social, and when we pair students, we invite them to listen to, respond to, and value each other’s thinking as they learn from and with each other. This means that during PAIR, students solidify their own ideas, get new ideas from their partners, and prepare to share thinking with the whole group.
Finally, students make their thinking visible to the whole class as they SHARE. The teacher invites a classmate to share ideas and strategies from their paired or small-group discussion. Because they are hearing from their classmates rather than the teacher, space opens for students to access new ideas or solidify their thinking.

In Quiet: The Power of Introverts in a World That Can’t Stop Talking, Susan Cain encourages us to add a “reflective pause” because our extroverts need to learn to listen, and our introverts need to learn to talk. Not all of my students initially felt this reflective pause would be useful to them, but when we framed quiet think time as a tool that would both enable introverted students to engage with a problem and prompt extroverted students to pause and reflect, my students became significantly more invested in the practice.
Beyond creating space for more introverted students and slowing the pace for those quick to answer, adding individual think time helped me address the needs of English learners and learners with disabilities, making our class a more engaging and equitable environment. In Routines for Reasoning, Grace Kelemanik, Amy Lucenta, and Susan Janssen Creighton note that
This extra processing time is . . . crucial for special populations. Some students with learning difficulties need extra time to retrieve stored information. English learners need extra time to find the English words to explain their ideas. Thus, think time can give students the opportunity to circumvent potential learning weaknesses and build on their strengths. (p. 23)
Learning to use and respect quiet think time was hard. We had a tight schedule to follow, a limited number of school days, and a lot of content to cover. If I only paid attention to covering content, how many of my students would have the opportunity to deeply interact with and understand both the content and their own thinking? I had to think deeply about what I wanted my students to experience in my classroom and the understanding I wanted them to leave with.
The shift to everyone contributing to our learning through the Think-Pair-Share routine was hard for my students, too. We’ve celebrated first and fast in our classrooms for too long, and in doing so, we’ve left some of our students behind. When students are used to being able to hide behind others, they aren’t used to sharing their thinking with others. It took time for some to risk putting their thinking into the room. What made the most difference for us was being explicit about why we were changing our practice, which came down to wanting everyone in our math community to contribute and everyone to learn.
IM hosted a summer math experience for students and teachers recently. Here’s a short video of a student reflecting on her experience using Think-Pair-Share.
Conclusion
Instructional routines such as Think-Pair-Share allow teachers to focus on eliciting and understanding our students’ thinking while giving students time to reflect on their thoughts and strategies. They are practices that we, and our students, experience, learn, and perfect over time. Instructional routines are ideal for teachers at any stage—they compliment the great classroom practices we’re already using, and they are easy to infuse with our own teaching styles.
Next Steps
While you consider enacting Think-Pair-Share in your classroom, you might reflect on:
- How can I create space for students to share their thinking?
- How can I encourage the class to value the ideas of others?
- How can I keep student thinking at the center of my instruction?
Download and print a Think-Pair-Share poster for your classroom at imk12.org/TPSposters.
 Jennifer Wilson
Jennifer Wilson
Senior Director, Implementation Portfolio
Jennifer Wilson (she/her) of Black Mountain, NC, enjoys learning alongside the Illustrative Mathematics community as the Senior Director, Implementation Portfolio. She is a National Board Certified teacher, and she taught and learned mathematics with students and teachers in Mississippi for 25 years. She is a recipient of the Presidential Award for Excellence in Mathematics and Science Teaching (2011) and has blogged at Easing the Hurry Syndrome and The Slow Math Movement. Jennifer thinks a lot about how we might slow down and savor learning math through curiosity, collaboration, and connections.
